How To Calculate The Rate Of Return On Any Investment

Introduction

Investing is where you try to grow your money by buying and selling different assets, such as stocks, bonds, mutual funds, and real estate. You spend money on fees, taxes, and research and earn from dividends, interest, and capital gains. So, how do you determine the rate of return on your investments? How do you compare the performance of different assets and decide which ones to buy or sell next? This is where you need to use some math and logic.

But what if you have many investments with different amounts and periods? How can you find the average rate of return for your entire portfolio? This is where you need to use the weighted arithmetic mean (WAM).

In this article, we will explain how to calculate the rate of return and the WAM for different types of investments, such as stocks, bonds, mutual funds, and real estate. We will also show you some examples and tips to help you understand and apply these concepts in your financial decisions.

What is the Rate of Return (ROR) on investment?

Rate of Return (ROR) on investment measures how much money you make or lose compared to how much money you invested in the first place. It is usually expressed as a percentage, so you can easily compare investments with the same maturities.

For example, if you invest Rs. 100 in a business and after a year you get back Rs. 120, your ROR is 20% because you made a Rs. 20 profit on your Rs. 100 investment. But if you invest Rs. 100 in another business and after a year you get back only Rs. 80, your rate of return is -20% because you lost Rs. 20 on your Rs. 100 investment.

To calculate the Rate of Return, you need to know your investment’s initial and current value and any income or expenses that occurred during the investment period. The formula for ROR is:

Rate of Return (ROR) = (Maturity Vale of Investment- Initial Investment)/Initial Investment * 100

Say, you bought stocks of Company A for Rs. 50, and you decide to sell the stock at Rs. 80/- after receiving a dividend of Rs. 10. Then your rate of return would be

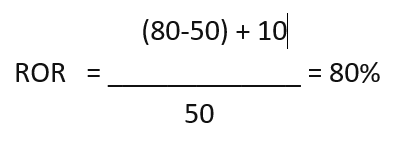
How to Calculate the Rate of Return (ROR) on Investments With Different Holding Periods?

The ROR tells you how well or poorly your investment performed over a certain period. But, the limitation of the above formula is that you can compare and calculate the absolute rate of return (ROR) of investments maturing within one year.

If you have investments with different holding periods, you must calculate annualized return on investment to compare investments with different periods. This will tell you how much your investment would grow or shrink each year on average.

The formula for annualized Rate of Return in this case is:

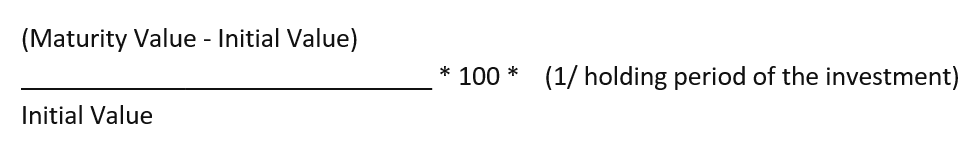
Let us understand Annualized Rate of Return with the help of an example. Say you invest Rs. 1000 in a bond for 10 years and receive Rs. 5000 on maturity; then your annualized ROR will be

AROR = [(5000 – 1000) / 1000] *100 * (1/10)  =  40%

What is the Weighted Arithmetic Mean (WAM) on investments?

WAM is a way of calculating the average rate of return or value of a portfolio of different assets, considering how much each investment contributes. It differs from the simple arithmetic mean, which treats all assets equally and does not reflect their relative importance or risk.

To calculate the weighted arithmetic mean, you need to assign a weight to each asset in the portfolio, representing its proportion of the total value or amount invested. The weight can be expressed as a fraction, a percentage, or a decimal. Then, you must multiply each asset’s return or value by weight and add all the products. Finally, you must divide the sum by the total of all the weights.

Weighted Arithmetic Mean helps you calculate the average rate of return on your portfolio comprising various financial instruments. You make better-informed investment decisions as it accounts for different market scenarios.

How to Calculate Weighted Arithmetic Mean (WAM) on Investment?

Weighted Arithmetic Mean is simply calculated as the weighted sum of the asset divided by the sum of the weights.

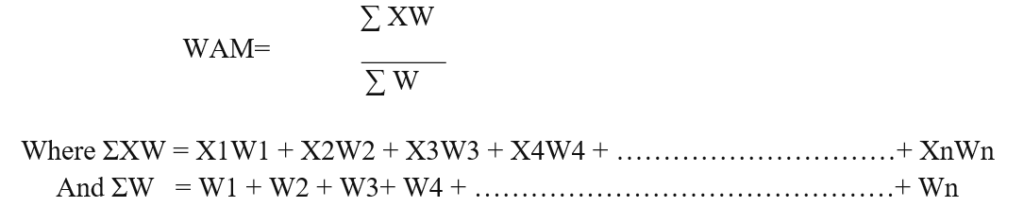
Calculating Rate of Return On Investments With Same Maturities

Suppose you have a portfolio of three investments: A, B, and C. You invested Rs. 20,000 in A, Rs 30,000 in B, and Rs. 50,000 in C. The total value of your portfolio is Rs. 100,000. The returns of each investment over one year are 10%, 15%, and 5%, respectively.

To calculate the weighted average rate of return of your portfolio, follow these steps:

• Step 1: Find the weight of each investment by dividing its value by the portfolio’s total value

For A, the weight is Rs. 20,000 / Rs. 100,000 = 0.2 or 20%. | For B, the weight is Rs. 30,000 / Rs. 100,000 = 0.3 or 30% | For C, the weight is Rs. 50,000 / Rs. 100,000 = 0.5 or 50%.

• Step 2: Multiply each investment’s return by its weight

The product is 0.2 x 10% = 0.02 or 2% for A. | For B, the product is 0.3 x 15% = 0.045 or 4.5% | The product is 0.5 x 5% = 0.025 or 2.5% for C.

• Step 3: Add up all the products: The sum is 0.02 + 0.045 + 0.025 = 0.09 or 9%

• Step 4: Divide the sum by the total of all the weights: The total is: 0.2 + 0.3 + 0.5 = 1 or 100%. The quotient is 0.09 / 1 = 0.09 or 9%. Therefore, the WAM rate of return of your portfolio is 9%.

Illustration to Help You Calculate the Rate of Return on Your Investments in Different Market Scenarios

Let us take another example to compare two stocks using the weighted arithmetic mean. You must know each stock’s expected rate of return under different market scenarios and the probabilities of those scenarios.

The stock with the higher weighted arithmetic mean has a higher expected rate of return. For example, suppose you have two stocks, X and Y, and their rate of returns in different market scenarios are as follows:

Market Scenario	Probability	Return of X(%)	Return of Y(%)
Boom	0.2	20	15
Normal	0.6	10	12
Recession	0.2	-5	-10

The weighted arithmetic mean of the returns for stock X is

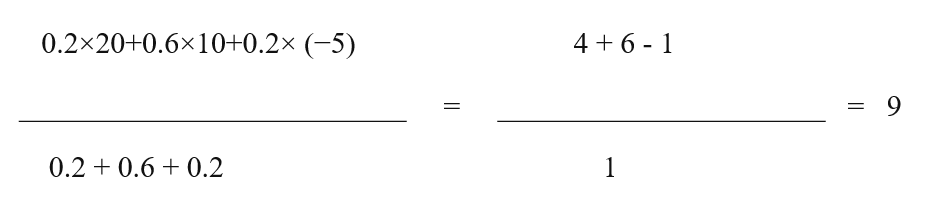
The weighted arithmetic mean of the returns for stock Y is:

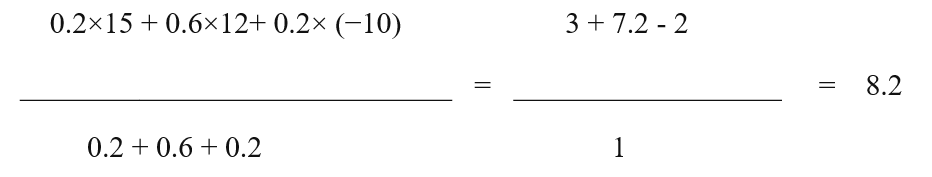
Therefore, stock X has a higher expected rate of return than stock Y, based on the weighted arithmetic mean. However, this does not mean that stock X is always better than stock Y because there are other factors to consider, such as risk, volatility, dividends, growth potential, etc.

The weighted arithmetic mean only gives you an estimate of the average rate of return under different market scenarios. Still, it does not account for the variability or uncertainty of those returns. You may also want to look at other aspects, such as the fundamentals and the technical ratios, and a lot more to get a complete picture of the performance of each stock.

Key Takeaways

The rate of return is a valuable measure of an investment’s profitability and performance over time. However, the rate of return can vary depending on the market scenarios and the probabilities of those scenarios.

To account for that, we can use the weighted arithmetic mean, which assigns different weights to each return based on its likelihood. The weighted arithmetic mean can help us compare investments with different maturities and risks, but it is not the only measure we should consider. It can also help you adjust your portfolio allocation according to your goals and preferences.

We should also look at other factors, such as the time value of money, the opportunity cost, and the variability of the returns, to make informed and rational investment decisions.

FAQs

Read more:  How Long-term investing helps create life-changing wealth – TOI.